Leetcode Single Number 问题总结

发表于 | | 阅读次数:
Leetcode上single number问题的总结

本文是single number问题的方法总结，重点会分析如何理解位操作的通用解法。

Single Number

首先来看第一个问题，问题描述是：

Given a non-empty array of integers, every element appears twice except for one. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:

Input: [2,2,1]
Output: 1
Example 2:

Input: [4,1,2,1,2]
Output: 4

不难想到，从数学的角度考虑，用两倍所有非重复元素和减去原数组即可，而且在python中，去除list中重复的元素转为set就可实现。
下面是对应的代码：

1
2
3
4
5
6
def singleNumber(self, nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    return 2 * sum(set(nums)) - sum(nums)

除此之外，我们还可以用位操作的方法来解决，所以这个题被分类到了位操作中。

对于这个题我们可以对每个元素用按位亦或操作^(相同位0，不同为1)，这样出现两次的元素在按位亦或的操作就会使对应位为0，
那么在遍历所有元素之后，结果就是那个只出现一次的数，相当于0^single_number。

对应的python代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
def singleNumber(self, nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    res = 0
    for i in nums:
        res ^= i
    return res
    # import functools
    # import operator
    # reduce functools.reduce(operator.xor, nums)

single number II

首先，问题描述是：

Given a non-empty array of integers, every element appears three times except for one, which appears exactly once. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:

Input: [2,2,3,2]
Output: 3
Example 2:

Input: [0,1,0,1,0,1,99]
Output: 99

和上一题一样，我们还是可以用求和的方法来解决，这个思路也可推广到任意参数为k,p问题：输入数组每个元素都出现了k次，只有一个只出现了p次，求那个单独的只出现p次的数。

但是位操作的方法就不是那么容易想到了，我这种渣渣自然是想不到的，但是看到讨论区有大神给出了详细的解释，但是篇幅比较长而且是英文，我这里就用中文解释一下。从第一个问题中我们可以大概看出，解决这类问题的关键是，遍历所有元素，进行某种reduce操作，这种操作要具有周期性，那么遍历之后的数就是我们要找的single number。比如在第一个题目中使用的是亦或操作，一个数如果出现偶数次那么亦或之后就会变成0，那么对于k为偶数，p为奇数的题我们都可以用相同方法解决。所以对于此题，我们要找到某种操作使得一个数出现k次之后又会重新回到最初的状态，类似于状态机的概念。直接可能很难想到，没关系，我们一步一步来。

首先考虑一个相对简单的问题，加入输入数组里面只有0和1，我们要统计1出现的次数，当遇到1就次数加1，遇到0就不变当次数达到k时，统计次数又回归到0。我们可以用m位来做这个计数工作，即$x_m, x_{m-1}, \ldots, x_1$，只需要确保$2^m > k$即可，接下来我们要考虑的问题就是，在每一次check元素的时候，做什么操作可以满足上述的条件。在开始计数之前，每一个计数位都初始化位0，然后遍历nums，直到遇到第一个1，此时$x_1$会变成1，继续遍历，直到遇到第二个1，此时$x_1=0, x_2=1$，直到这里应该可以看出规律了。每遇到一个1，对于$x_m, x_{m-1}, \ldots, x_1$，只有之前的所有位都为1的时候才需要改变自己的值，如果本来是1，就变成0，本来是0，就变成1 ，如果遇到的是0，就保持不变。搞清楚了这个逻辑，写出表达式就不难了。这里以m=3为例给出python代码：

1
2
3
4
5
for i in nums:
    x3 ^= x2 & x1 & i
    x2 ^= x1 & i
    x1 ^= i
# other operations

但是到这里还没有解决当1的次数到k时，计数值要重新返回到0，也就是所有计数位都变成0这个问题。解决办法也是比较巧妙。

假设我们有一个标志变量，只有当计数值到k的时候这个标志变量才为0，其余情况下都是1，然后每一次check元素的时候都对每个计数位和标志变量做与操作，那么如果标志变量为0，也就是计数值为k的时候，所有位都会变成0， 反之，所有位都会保持不变，那么我们的目的也就达到了。

好，最后一个问题是怎么计算标志变量的值。将k转变为二进制，只有计数值达到k，所有计数位才会和k的二进制一样，所以只需要将k的二进制位做与操作，如果某个位为0，就与该位取反之后的值做与操作。

以k=3, m=2为例，简要的python代码如下：

1
2
3
mask = ~(y1 & y2) # where yj = xj if kj = 1, and yj = ~xj if kj = 0, k1, k2是k的二进制表示(j = 1 to 2).  
x2 &= mask;
x1 &= mask;

将这两部分合起来就是解决这个问题的完整算法了。

接下来要考虑的问题就是如何将这个问题推广到整数。我说这话的意思是这个算法确实可以推广到整数，假设我们用32位来表示一个整数，那么我们只需要将$x_m, x_{m-1}, \ldots, x_1$换成32的整数即可。下面给出这个推广的过程方便大家理解。

我们可以把32位分开来看，用32个m位计数器来统计对应位1的出现次数。换一种思路，我们也可以把这32个m位的计数器看成m个32位计数器。这里我们同样用$x_m, x_{m-1}, \ldots, x_1$来表示。

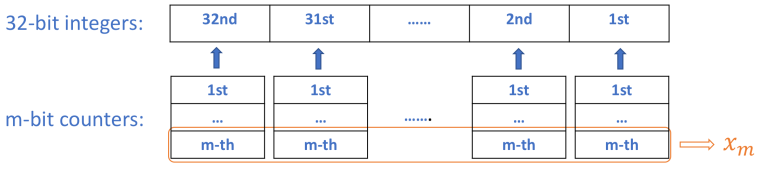
single number II

以$x_1$为例，其第r位的值由什么决定呢？显然是要数组中所有整数第r位1的出现次数来确定，这里用q表示，更具体的说是由$q’=q \% k$决定（因为每出现k次就会回到0），再具体一点，等于其二进制的第r位。而除开我们要找的single number,其余的数在计数结束之后，对m个计数器的值没有贡献，因为都出现p次，然后计数值归0，也就是说，计数器最后的每个位的值实际上是由single number的对应位1的次数决定的。前面已经说过，对于一般性的问题，假设single number出现的次数是p，当然p可以大于k，也可以小于k，由于我们设计的计数器的性质，出现k次等于归零，所以对最后计数器的值有贡献的只是p' = p % k。

那么，事情就很明朗了，我们把p'写成二进制形式，那么其中某一位为1，那么对应计数器的第r位就和single number的第r位一致。因为如果single number的第r位为0， 那么计数值为0，自然计数器的第r位也为0，如果为1，那么计数器的第r位就和p'的二进制对应位一致，也是1.

所以，在最后计数结束的时候，我们只需要返回p'二进制为1的对应计数器即可，其数值肯定是和single number的值相同。

以这个题目为例，k=3, p=2，那么m=2，也就是我们需要两个32位的计数器。而$p \% k$的二进制是10，那我们最后应该返回x2。对应的python代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        x1, x2, mask = 0, 0, 0
        for i in nums:
            x2 ^= x1 & i;
            x1 ^= i;
            mask = ~(x1 & x2);
            x2 &= mask;
            x1 &= mask;
        return x2

值得注意的是，这个方法的使用条件是p % k !=0，如果p是k的整数倍的话，这个方法是不适用的。

single number III

最后是single number问题的第二个变种，问题描述是：

Given an array of numbers nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.

Example:

Input: [1,2,1,3,2,5]
Output: [3,5]

Note:

The order of the result is not important. So in the above example, [5, 3] is also correct.
Your algorithm should run in linear runtime complexity. Could you implement it using only constant space complexity?

这次的问题变成special的数又两个了，实际上题目并不是找single number了，而是找special two number。所以之前两个题目的解法是不适用的，起码不是直接适用的。如果可以把two number的问题变成两个single number的问题，就可以套用之前第一个问题的解法了，也就是说我们可以通过某种方式把数组分为两组，每组只包含那两个special number中的一个。

问题的关键就变成如何分组了。思路也是有点巧妙，考虑到两个special number是不一样的，而恰好其余的数都是出现两次，所以如果对每个数都做亦或操作，最后的结果就是那两个special number的亦或，而且至少有一个位是1，那么就可以根据其中一个为1的位将所有的数分为两组，再套用第一个题的方法即可。

python实现的代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        xor = 0
        a = 0
        b = 0
        for num in nums:
            xor ^= num
        mask = 1
        while(xor&mask == 0):
            mask = mask << 1
        for num in nums:
            if num&mask:
                a ^= num
            else:
                b ^= num
        return [a, b]

同样，这类解法还是有局限性的，那就是两个special number出现的要是1，而且其余数出现的次数要是偶数。

总结

最后，我们对single number问题及其变种做一下总结：

  1. 用求和的方式是通用的解法
  2. 位操作方法是有局限的，对于不同的变种有不同解法，用位操作解决的关键是
  3. 利用相同的数偶数次按位亦或结果为0，计数次按位亦或是自身
  4. 灵活运用mask和与操作来改变或者检验某一位

参考

文章主要参考了讨论区的一片英文的帖子，如果英文好的可以去看下原文。

https://leetcode.com/problems/single-number-ii/discuss/43295/Detailed-explanation-and-generalization-of-the-bitwise-operation-method-for-single-numbers

有钱的捧个钱场，没钱的捧个人场